
| Online Argonauta |
<< Back to Index |
群集組成の多変量解析
| 大垣俊一 |
| 種A |
種B |
… |
種J |
|
|
|
||||
| St. 1 |
χ1A |
χ1B |
… |
χ1J |
| St. 2 |
χ2A |
χ2B |
χ2J |
|
| : |
: |
: |
: |
|
| St. 5 |
χ5A |
χ5B |
… |
χ5J |
|
|
||||
 |
[図1] |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Z1I = LIAχ1A + LIBχ1B + … + LIJχ1J (St 1の第I主成分)このとき、先に述べた主成分の理論的性質から、Lは次の条件を満たすように定める。
Z2I = LIAχ2A + LIBχ2B + … + LIJχ2J (St 2の第I主成分)
:
Z5I = LIAχ5A + LIBχ5B + … + LIJχ5J (St 5の第I主成分)
(Z1I−ZmI)2 + (Z2I−ZmI)2 + … + (Z5I−ZmI)2 が最大ここにZmIはZ1I, Z2I … Z5Iの平均であって、(Z1I−ZmI)2,… は偏差平方、これをたし合わせて全体のばらつきの指標となる。第2主成分以下も同様に{LIIA, LIIB, … LIIJ}{LIIIA, LIIIB, … LIIIJ}などを定めてゆくが、これらについては先の二つの条件のほか、その主成分が前のすべての主成分に対して独立であるために、ZII, ZIII… 軸が、前のすべての軸に直交する、という条件が加わる。そしてこのLの列の組、つまり、
LIA2 + LIB2 + … + LIJ2 = 1
という行列が定まれば、各Stの第I〜第X主成分がすべて計算できることになる。この、triangular matrixからLの行列を導くための計算は、偏微分や固有値が出てきて複雑であり、私は細部まで理解していない。しかしこの部分については教科書を信頼して、表2からLが求まることを納得すれば、各主成分とその寄与率が計算できることになる。実際の操作としては、コンピュータに表1のデータを打ち込み、相関行列と分散・共分散行列のどちらかを選択するだけである。
LIA
LIB
…
LIJ
LIIA
LIIB
…
:
:
LXA
LXB
…
LXJ
 |
[図2] |
 |
[図3] |
 |
[図4] |
|
St 1 |
St 2 |
差 |
差/X1+X2 |
|
|
|
||||
| 種A |
χ1A |
χ2A |
|χ1A−χ2A| |
δ12(A) |
| 種B |
χ1B |
χ2B |
|χ1B−χ2B| |
δ12(B) |
| 種J |
χ1J |
χ2J |
|χ1J−χ2J| |
δ12(B) |
|
|
||||
| 計 |
X1 |
X2 |
Σδ12 = Bray-Curtis Index |
|
|
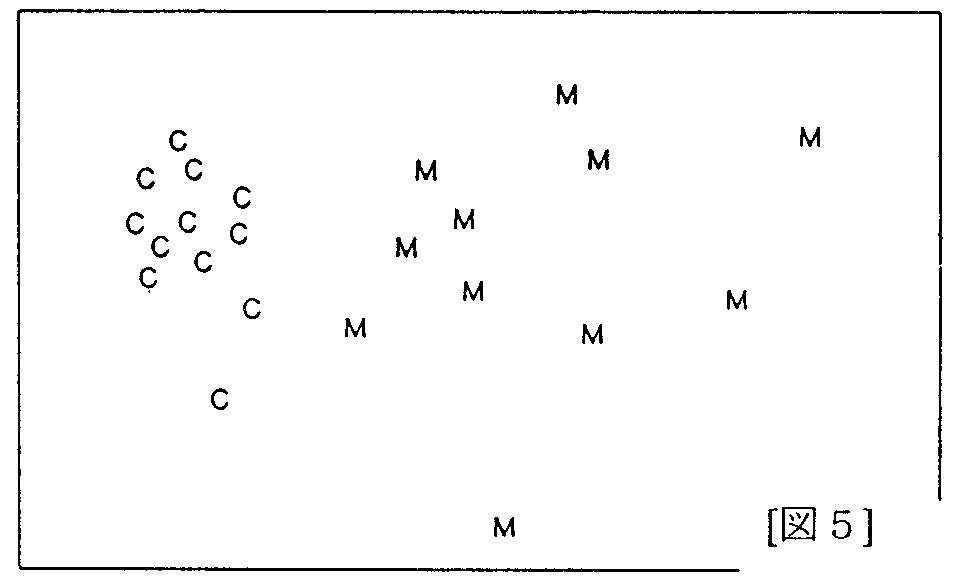 [図5] [図5]
|
|||||||||||||||||||||||||||||||||||
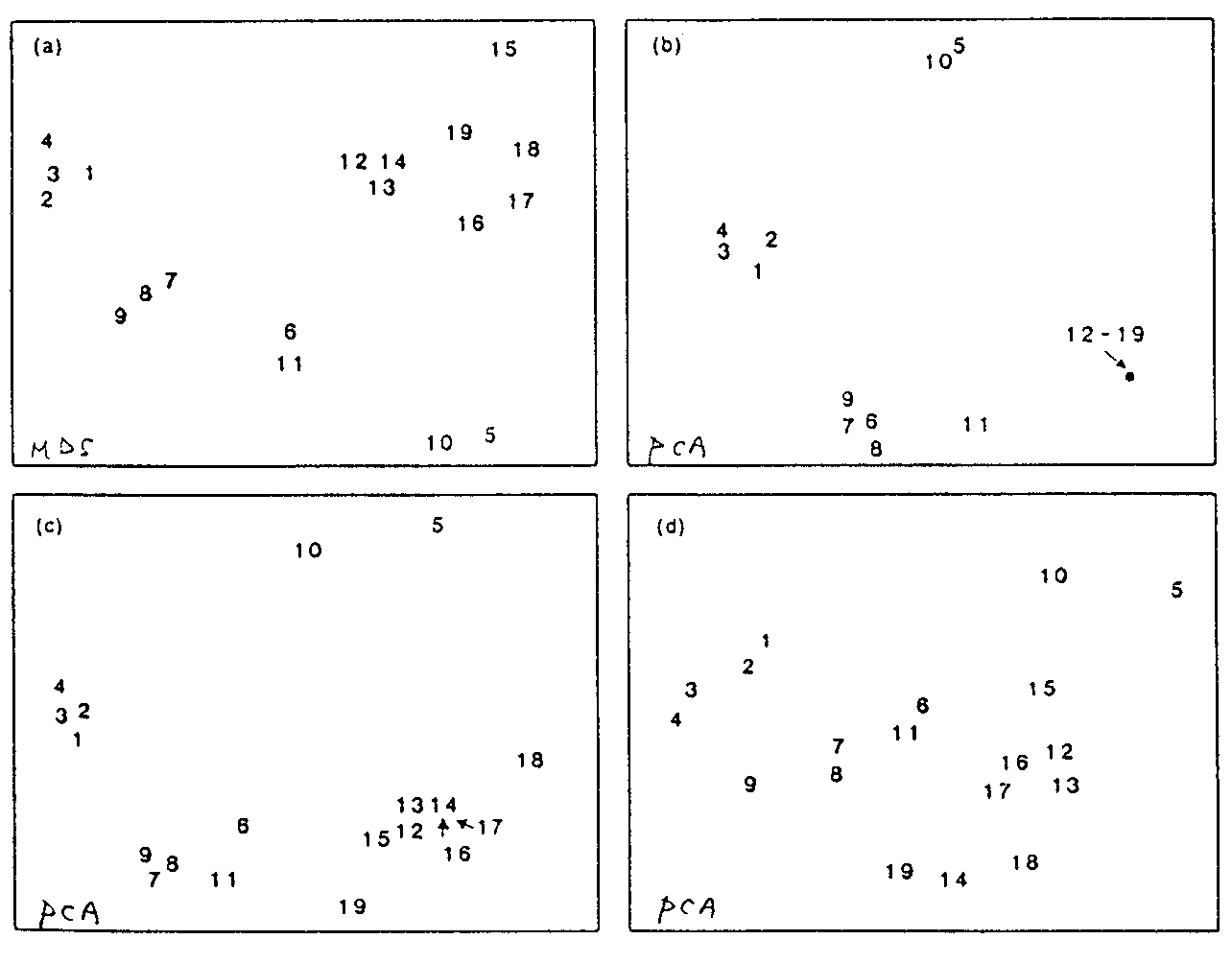 |
[図6] |
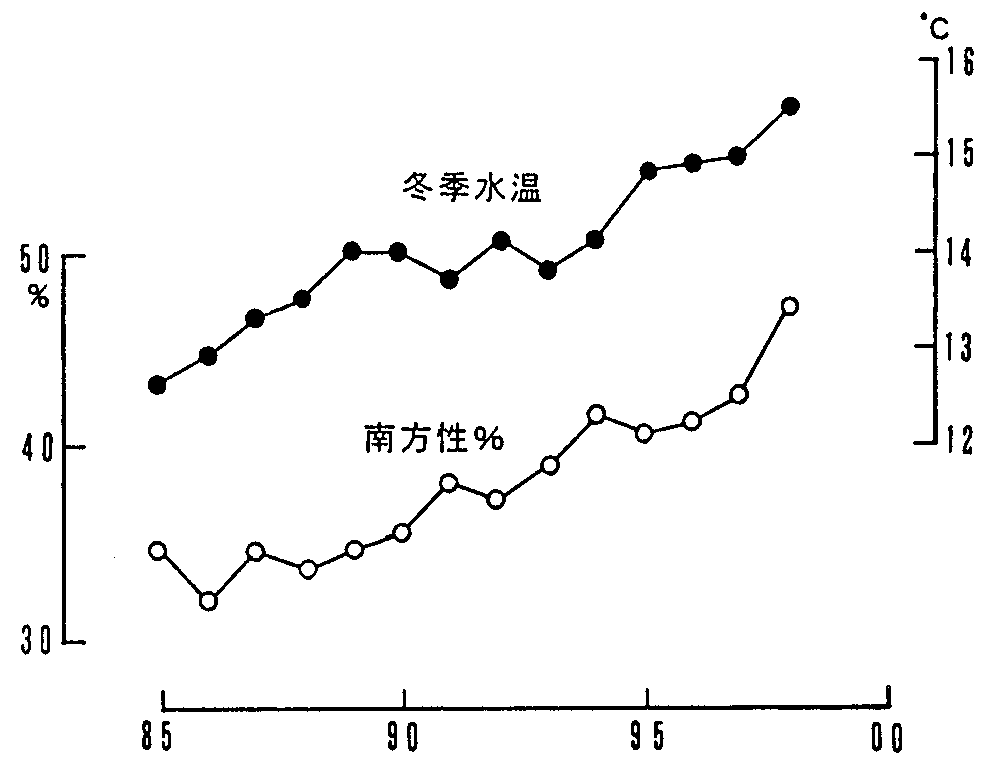 |
[図7] |
| Online Argonauta |
<< Back to Index |